The Polyhedrists (2022) – Review

The Polyhedrists is described as ‘a history of the relationship between art and geometry in early modern period’.[1] Despite it being a relatively short book, it offers a complex and confronting view of polyhedra’s history; polyhedra being three-dimensional convex shapes with flat polygonal faces and straight edges. Its author, Noam Andrews, presents the story of polyhedra from Erhard Ratdolt’s edition of Euclid’s Elements published in 1482 and the work of artists and artisans in creating a new language of forms—and their distillation of abstract ideas into objects—to the plethora of solids which constituted the basis of Renaissance mathematical knowledge.


The first two chapters, Rhombicosidodecahedron and Corpora Regulate et Irregulata introduce Andrews’ stance on the history of geometry and perspective, that contrary to contemporary thought, its development started before the Renaissance. Rhombicosidodecahedron acts as an introduction, outlining the narrative arc of the book, and showing the span of interest and the field of experimentation across the late 15th and 16th centuries. Corpora Regulate et Irregulata builds on this, charting the movement of polyhedra into a visual form, working out of the limited language of mathematics into palpable objects. It is here that we are introduced to the notions of regular and irregular corpora. The Platonic or regular solids, corpora regulate, are the potential forms derived by slicing up or embellishing regular polygons, in their case all the edges are congruent—Andrews cites the rhombicuboctahedron in Ugo da Carpi’s chiaroscuro woodcut print of Archimedes (c.1518–1520) as one of these forms. Whereas corpora irregulata operate upon the regular solids, formed by polygons having different shapes where all the elements are not the same—their amount is only limited by the imagination of polyhedrists. The period of exploration of these forms, both regular and irregular, shifts the way of communicating mathematical and perspectival concepts. This change is marked in Erhard Ratdolt’s reedition of Euclid’s extensive mathematical treatise Elements, originally written in 300 B.C., illustrated with explanatory diagrams by Ratdolt. It was the first text to employ illustrations and was in opposition to the Italian approach to mathematical texts, which exclusively used extensive descriptions.

Chapter three, Instruction in Measurement, focuses on the city of Nuremberg as a hotbed of polyhedral innovation due to its sophisticated print industry, and the graphic treatise of Albrecht Dürer including his Underweysung der Messung, published in 1525. Dürer, like Ratdolt, not only offered illustrations to his texts but also depicted nets of the forms which one could cut out and construct into physical forms. His treatise was a manifesto on the proper and exact use of geometry ‘made visual’, inviting the reader to partake in his ideas. Despite the work in putting the nets together, the treatise significantly advanced the discipline, no longer requiring an understanding of high-level terminology to decode an unillustrated text or the necessary set of artistic skills to be able to render the polyhedra in 2D. In a relatively simple move, Dürer made geometry easier, more accessible and understandable.
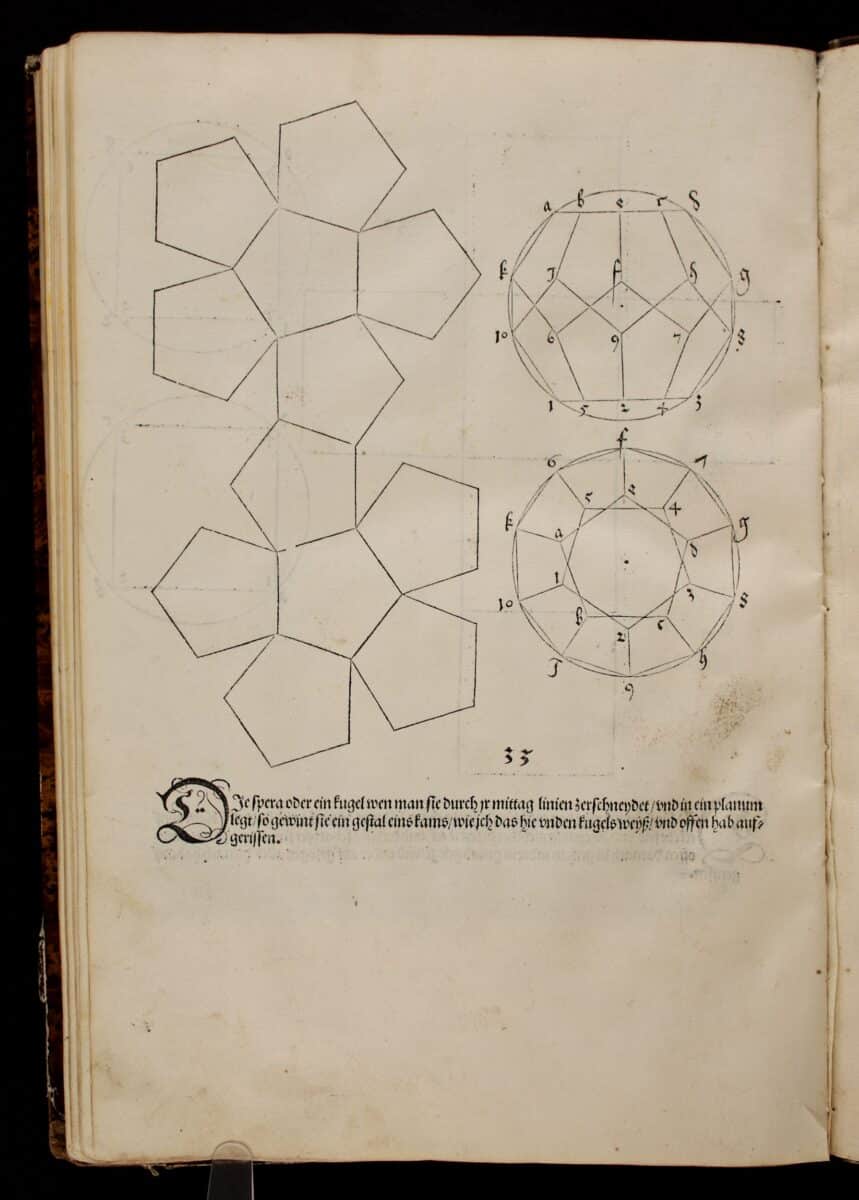
Andrews continues focusing on southern Germany throughout the book, and in chapter four, Geometria and Lehrbuch, the dissemination of geometric principles in Nuremberg is discussed again. But this time through the wider reach of mathematical ‘manuals’ known as Lehrbücher. The author first discusses the changes that occurred in the teaching environment of universities by figures like Philip Melanchthon. Melanchthon brought a humanist curriculum to the University of Wittenberg, which focused on the underlying natural and divine order of all things, working off Aristotelian philosophy, and relying on ancient texts, like Euclid’s Elements. Andrew places the Lehrbücher, the image-rich manual of the artisans of Nuremberg in opposition to the fairly static Elements. Craft was a highly regarded commodity in the 16th century, but craftsmen did not have access to the ‘higher knowledge’ of university mathematics courses. Working with Dürer’s treatise the craftsmen presented illustrated geometric concepts based on the local skills. Craftsmen became a vital network of informal learning that widened mathematical imagination, shifting attention from the academic approach to a physical one.

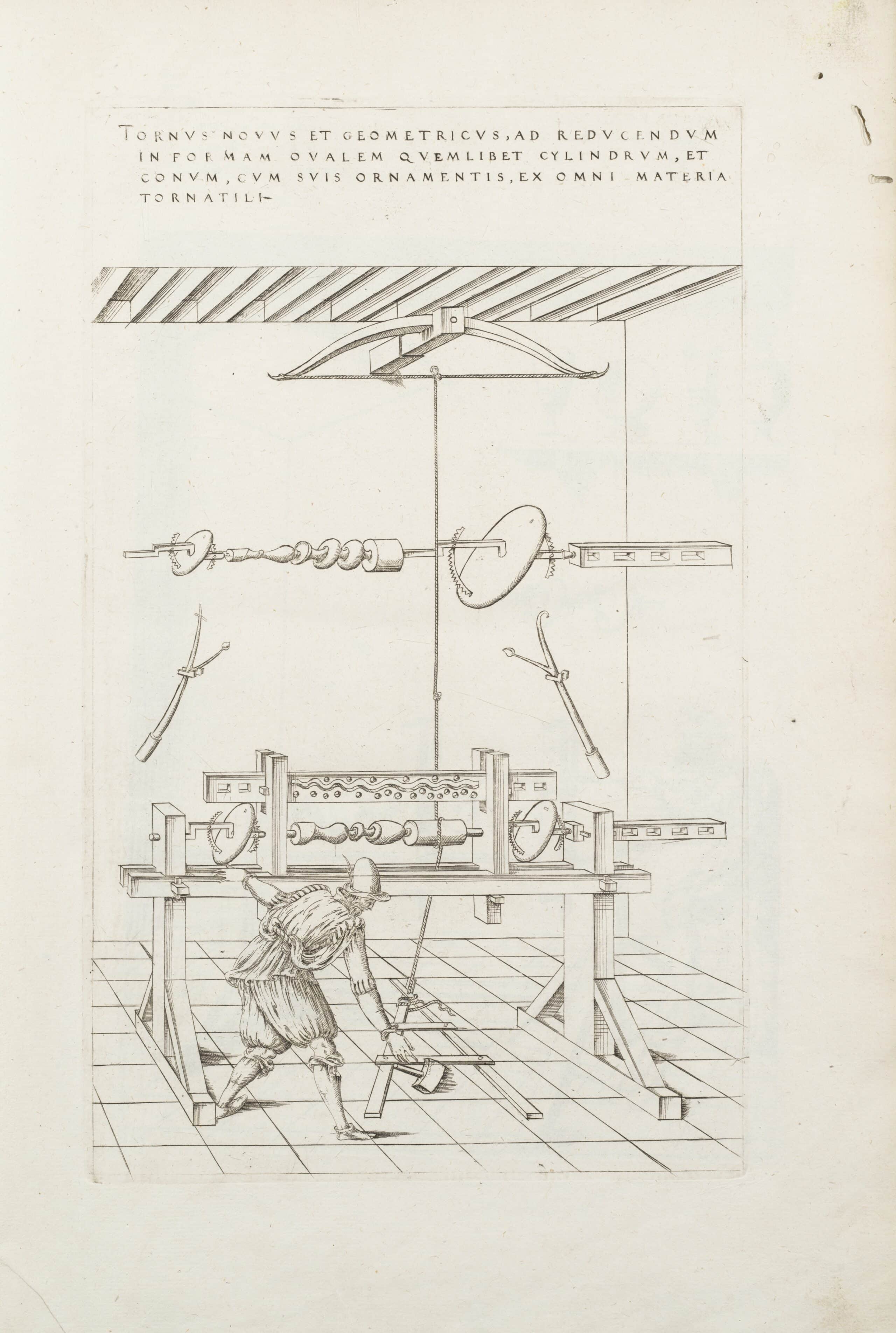
Chapters five and six, Lover of the Art of Perspective and Cut Apart in Many Ways explore this experimentation of polyhedra in the work of craftsmen. Through the making of their objects the scientific form is made decorative—with the goldsmith designs of Wenzel Jamnitzer and the prints of Lorenz Stöer are highlighted here. The penultimate chapter, The Violence of Whimsy, also views craft as the driving force of polyhedra in the period. Andrews describes the innovation in lathe design which enabled artisans to create more complex polyhedral structures, such as ivory towers of shapes within shapes.

The epilogue consolidates all these developments and reflects on the role of polyhedrists in mathematical history: a field shaped by the imagination and experimentation of craftsmen and artisans. The popularity of polyhedrists came from their application, not their theory. The book ends with the transition of the discipline back into academia, and its eventual aid as the basis of the work of Kepler and Descartes.
The book beautifully layers the history of polyhedra, each chapter carefully overlaying people, places, texts, and drawings, to convey the progressions of the period. Noam Andrews communicates the transition of mathematics with ease, from the limited academic text to the treatise, illustrated by drawings and nets, to its plethora of physical manifestations. He makes apparent that this change was not an ideological one, at the highest levels of academic thought, but formed through an informal network of publications and objects.
Approaching The Polyhedrists from an art historical background, it allowed me to enter into the world of these multifaceted forms, elegantly dissecting the complex and undecipherable world of mathematics.
Noam Andrews, The Polyhedrists: Art and Geometry in the Long Sixteenth Century is published by MIT Press. Copies of the book can be purchased here.
Rosie Ellison-Balaam is an editor at Drawing Matter.
Notes
- https://mitpress.mit.edu/9780262046640/the-polyhedrists/ [accessed 05.12.23].
