Onto an Epicycle of Cones

This drawing is part of a series that interrogates the orthographic drawing techniques of Guarino Guarini (1624–1683) set out in his posthumous treatise, Architettura civile, (1737). While some of the drawings from the series deal with the direct documentation of his orthographic drawings, this particular drawing translates his written and drawn instructions in the programming language of Python in the open-source platform of Processing.py. The objective of the drawing and research in general, is to use historically and seemingly defunct modes of architectural drawing to reimagine digital tools.
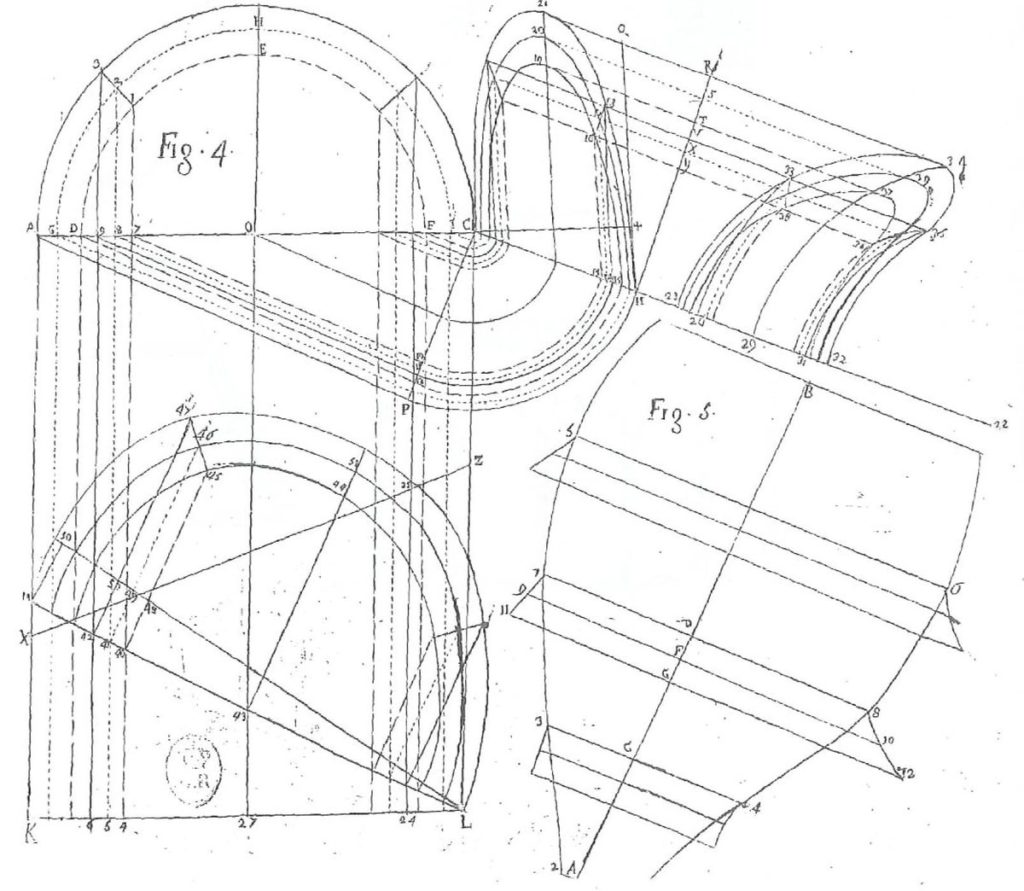
The drawing process is derived from Guarini’s technique for translating the geometry of three-dimensional vaults into two-dimensional stone cutting templates. An example of this can be found in Tractate 4, Lastra 4, Figures 4-5. Guarini provides the method for developing a vault from the projection of a semicircle onto an oblique plane and a cone. For the cone, Guarini reminds the reader that the section of a cone parallel to its base is a circle. He then measures the radius of each circular section in top view of the projection. These radii are used to plot the curve of the distorted semicircle in front view. The distances found in front view are then used to unroll the vault onto a flat plane in figure 5.
In an analogous manner, Onto an Epicycle of cones begins with the projection of semi-circle onto the vertical section of a cone at its axis—a triangle. The circular or elliptical conic sections at each point of intersection with the triangle are measured and then used to locate the projection of the same intersections in top view. Variation and motion are then introduced to the drawing by two means. The first introduces variation by changing the radius of the semicircle and the orientation and size of the cone over time. This allows the projection to both grow in size, but also shift in form as the conic sections change from circular to elliptical. The second uses the defunct model of planetary motion, the epicycle, to displace the top view projection over time in three related epicycles rotating at varying rates. The process is nearly identical to Guarini’s except that in lieu of single cone, there are many.
There are three zero-degree oblique projections extending out from the center of the drawing. Each of the projections isolates the geometric results of the epicycles in three sets of intersecting barrel vaults. The position of the projections is indexical of the rate of change of the epicycle that they are drawn from. The three oblique projections serve as the base for orthographically unrolling the sets of intersecting barrel vaults.
The drawing uses a single colour expressed in values of red, green and blue which are scaled across different lines within the drawing until they approach the value corresponding to white. Line weight corresponds to the conventions of descriptive geometry in which object lines are thicker and construction lines are thinner. The entire drawing is confined to operations on a two-dimensional plane. There are no surfaces, three-dimensional objects, or three-value coordinates. The drawing is a two-dimensional orthographic projection.
