Relics of Electronic Hallucinations
Gazing at Early Computational Fluid Dynamics Drawings from the Los Alamos Scientific Laboratory
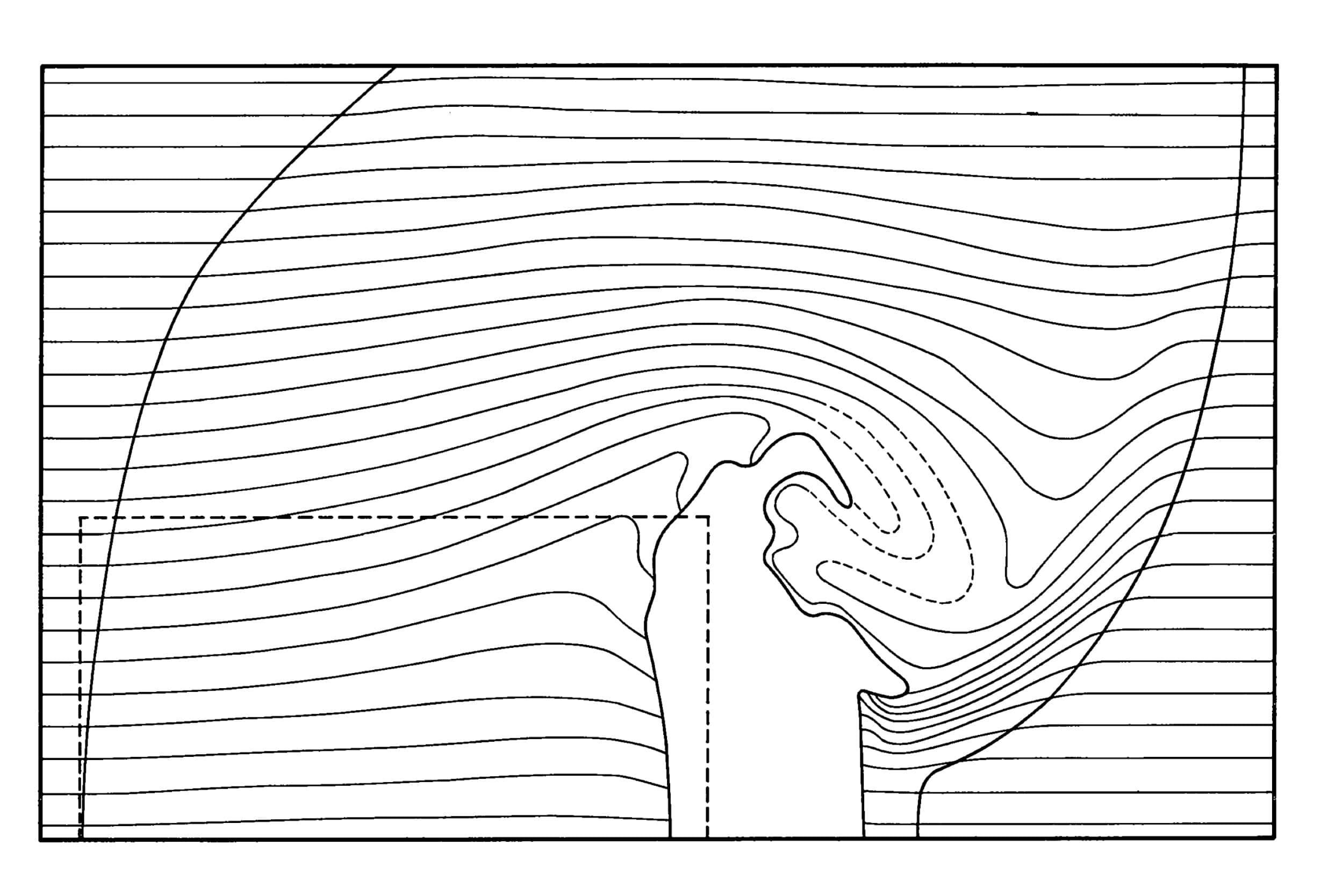
During the 1950s and 1960s, the T-3 research group at the Los Alamos Scientific Laboratory produced the first drawings of what is now known as computational fluid dynamics. Using the prowess of early electronic computers—initially developed for the Manhattan Project, the T-3 group, working under the auspices of the U.S. Atomic Energy Commission—successfully simulated and visualised the complex behaviour of fluids and gases in virtual environments. These drawings—some of which are presented here—allowed the scientists to understand the phenomena of shockwaves and high-speed collisions under which solids deform, liquify or vaporise—without having to conduct the experiments in the real world. Plotted by early electro-mechanical plotters and attached to the laboratory’s scientific reports, the drawings were done by means of mass calculations, creating and observing realities and spaces that did not physically exist.[1]




Looking at the drawings seventy-odd years after their conception, one is stricken by their strange and somewhat ominous beauty. As relics from Los Alamos, a central place during the rise of the nuclear era, computation and cybernetics, these drawings encapsulate the embryonic traces of what is arguably a radical shift in the cognition and representation of space.[2] Space is structured here as a dense, interconnected network of cells, where each cell has the potential of movement, depending on its configuration in the network and the information it receives and transmits to its neighbouring cells. The image results from the unpredictable process of interaction between the network’s cellular components, positioning and arranging clusters of points according to the information it calculates. Drawing thus emerges not from a single source of inscription or authorship, but as a flicker in a constant flow of information discharged by an autonomous system. Is it incidental that the observation of fluid dynamics was facilitated by a drawing system fluid in its nature?[3]

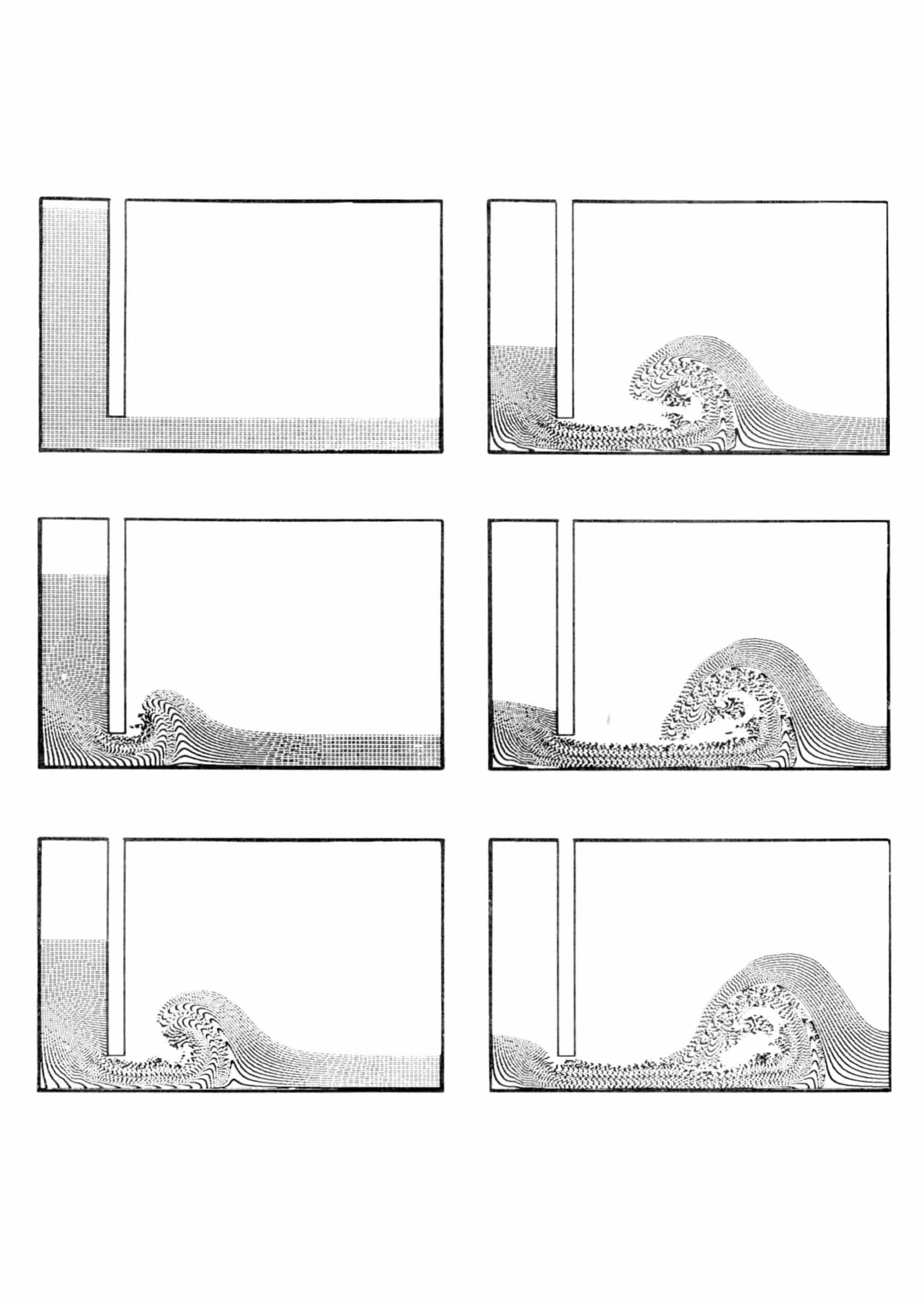
Vilém Flusser attempted to grasp this rapture in the realm of representation by postulating that ‘the difference between traditional and technical images would be this: the first are observations of objects, the second computations of concepts. The first arises through depiction, the second through a peculiar hallucinatory power that has lost its faith in rules.’[4] Exemplifying Flusser’s hypothesis, the T-3 group drawings are indeed computations turned into images, produced in a manner that lies beyond our senses, detached from optics, haptics or any form of corporeal knowledge. They are visual interpretations of concepts that exist primarily as electric signals inside a machine. Unlike the scientific images produced by Santiago R. y Cajal, Alexander von Humboldt or Étienne-Jules Marey, the realities that the T-3 group drawings describe—in which solid objects violently deform, liquify and melt into air—were constructed through hidden mechanisms of an analogous process, not by direct sensorial observation. In other words, the scientists of the T-3 group visualised a reality through a process which could be described as an electronically induced hallucination.

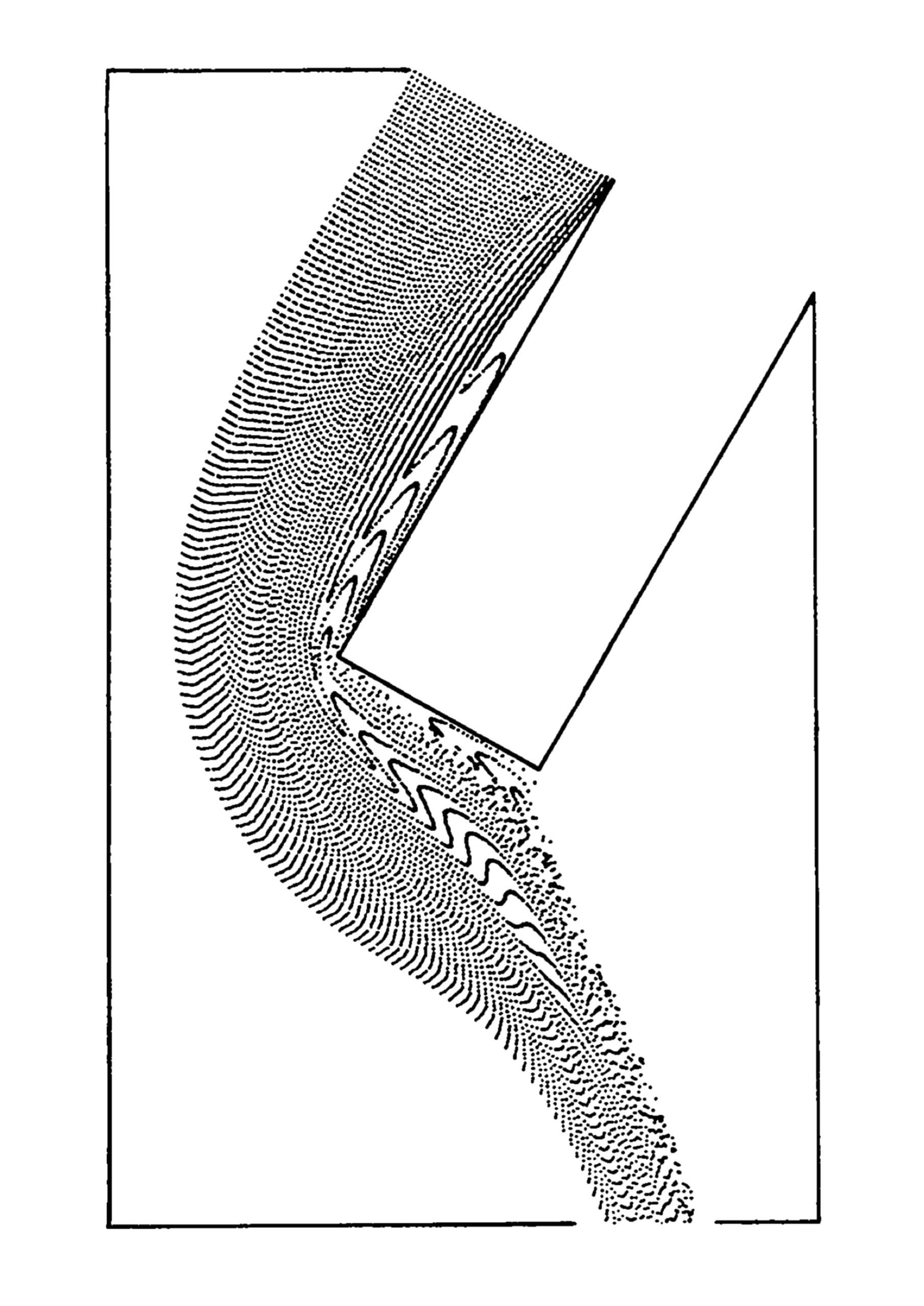
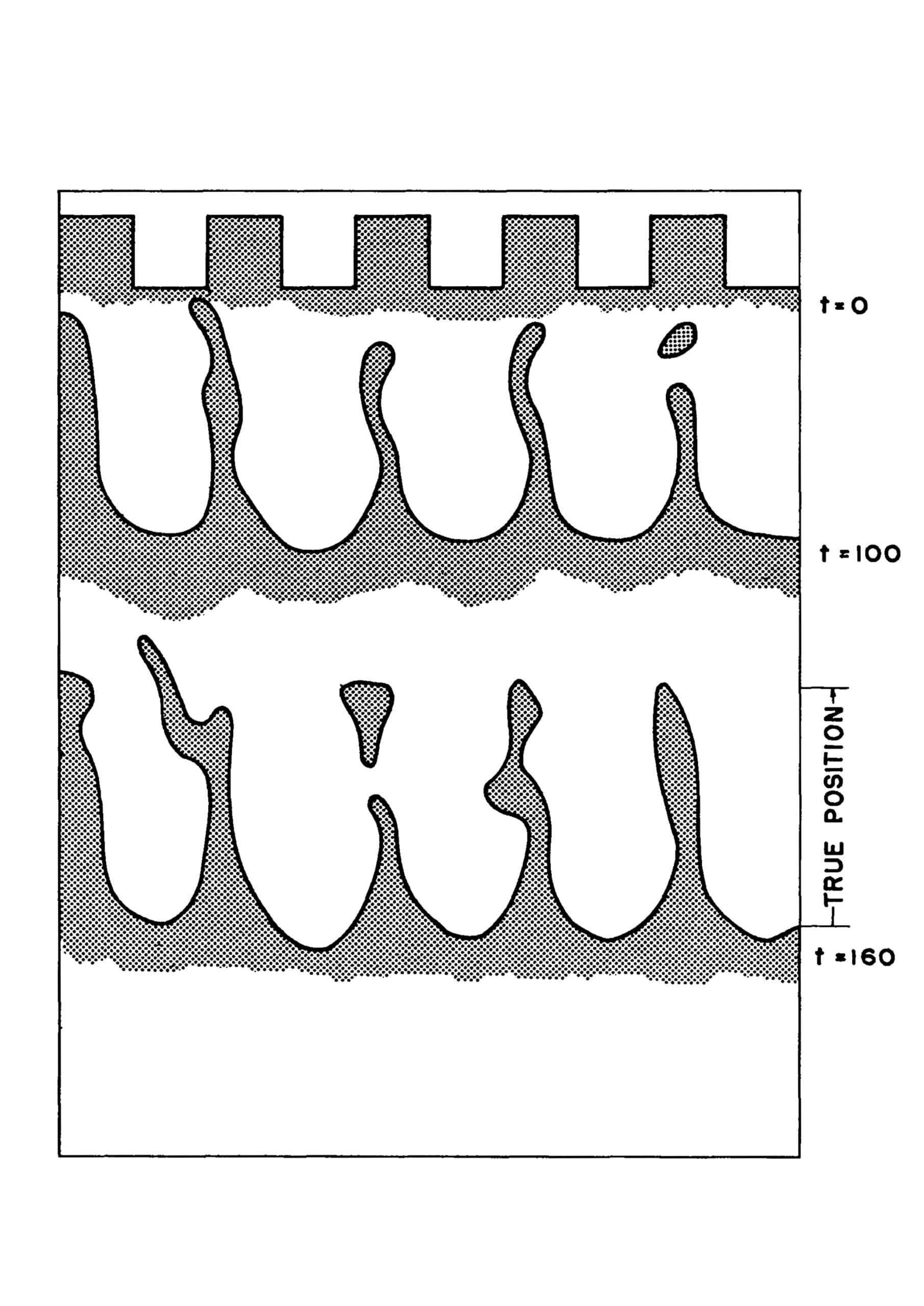
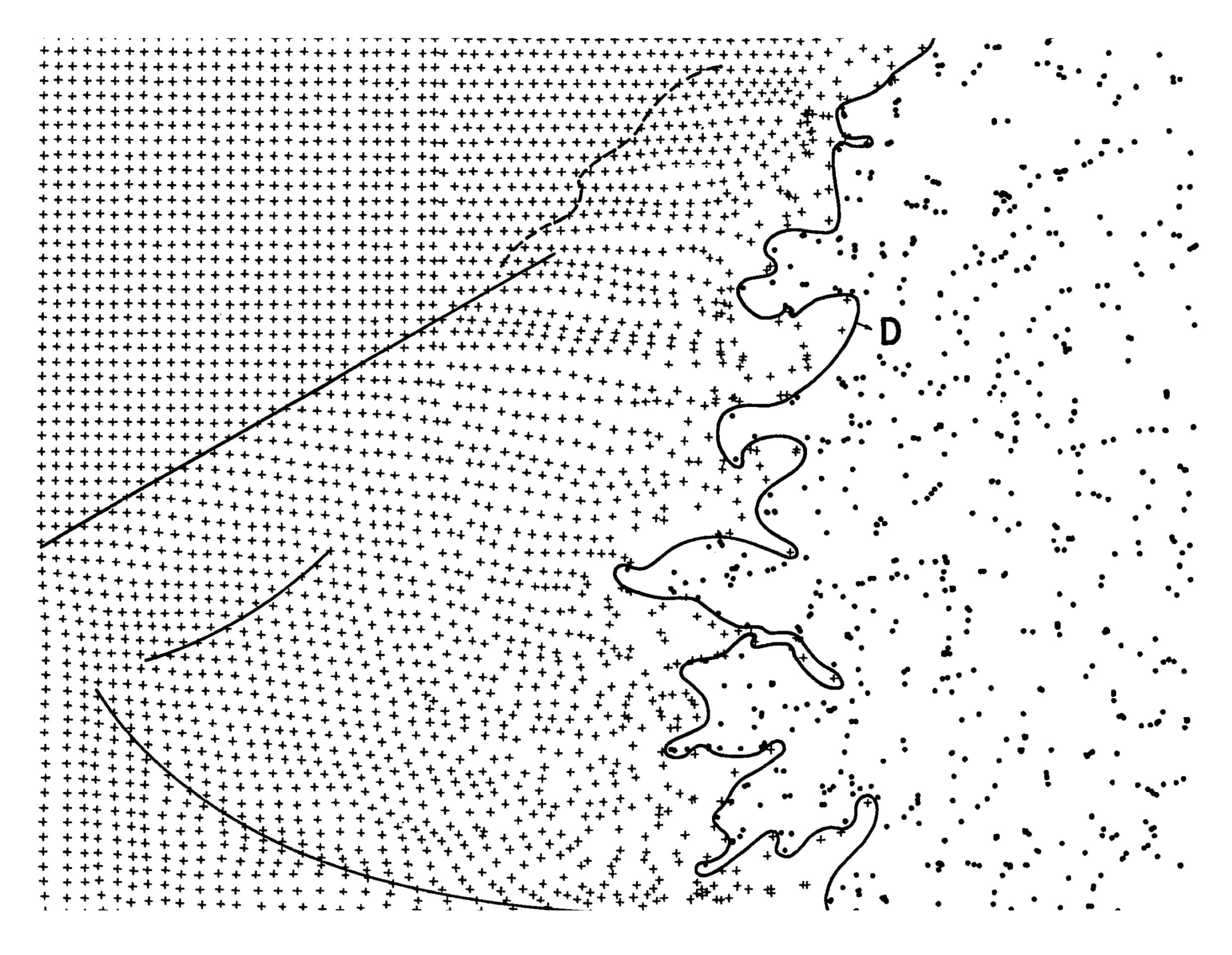
Looking closely, one can sense a dose of hallucination in the drawings themselves. Figures and space, while measured with extreme accuracy, seem to be in a constant state of diffusion: traditional drawing dichotomies of solid/void or background/foreground dissolve and transform into a flux of ambiguous in-between states. The particularities of space are made legible not by orthographic delineation but through painterly gestures of densities and gradients that have no absolute boundaries or definitive position. Looking at the T-3 group drawings, we witness the outset of a slow withdrawal from the orthodoxy of projective geometry as the sole arbiter of measured space, and the emergence of what one might call a form of cloud-gazing; peering into a space that ‘lost its faith in rules’ but perhaps celebrates that loss as a type of liberation.[5]
Notes
- Francis H. Harlow, ‘Fluid Dynamics in Group T-3 Los Alamos National Laboratory’, Journal of Computational Physics, 195, no. 2 (April 2004), 414–33.
- Heinz Von Foerster notes, ‘I propose to interpret cognitive processes as never ending recursive processes of computation.’ Heinz Von Foerster, Understanding Understanding: Essays on Cybernetics and Cognition, (New York: Springer, 2003),10.
- Lebbeus Woods succinctly discusses contemporary social, technological and architectural notions of fluidity in: Lebbeus Woods, Fluid Space, The Lebbeus Woods Blog, 28 June 2009, <https://lebbeuswoods.wordpress.com/2009/06/28/fluid-space/> [accessed 20 May 2024]
- Vilém Flusser, Into the Universe of Technical Images, trans. by Nancy Ann Roth (Minneapolis: University of Minnesota Press, 2011), 10.
- Ibid.
Uri Wegman is an architect and an educator. He taught at the Cooper Union, New York, EPFL, Lausanne and currently at La Cambre- Horta School of Architecture in Brussels where he is also conducting research about the representation of air in architecture. He is a co-founder of the Truant School, an independent platform for research, production and education.
