– Stacey Lewis

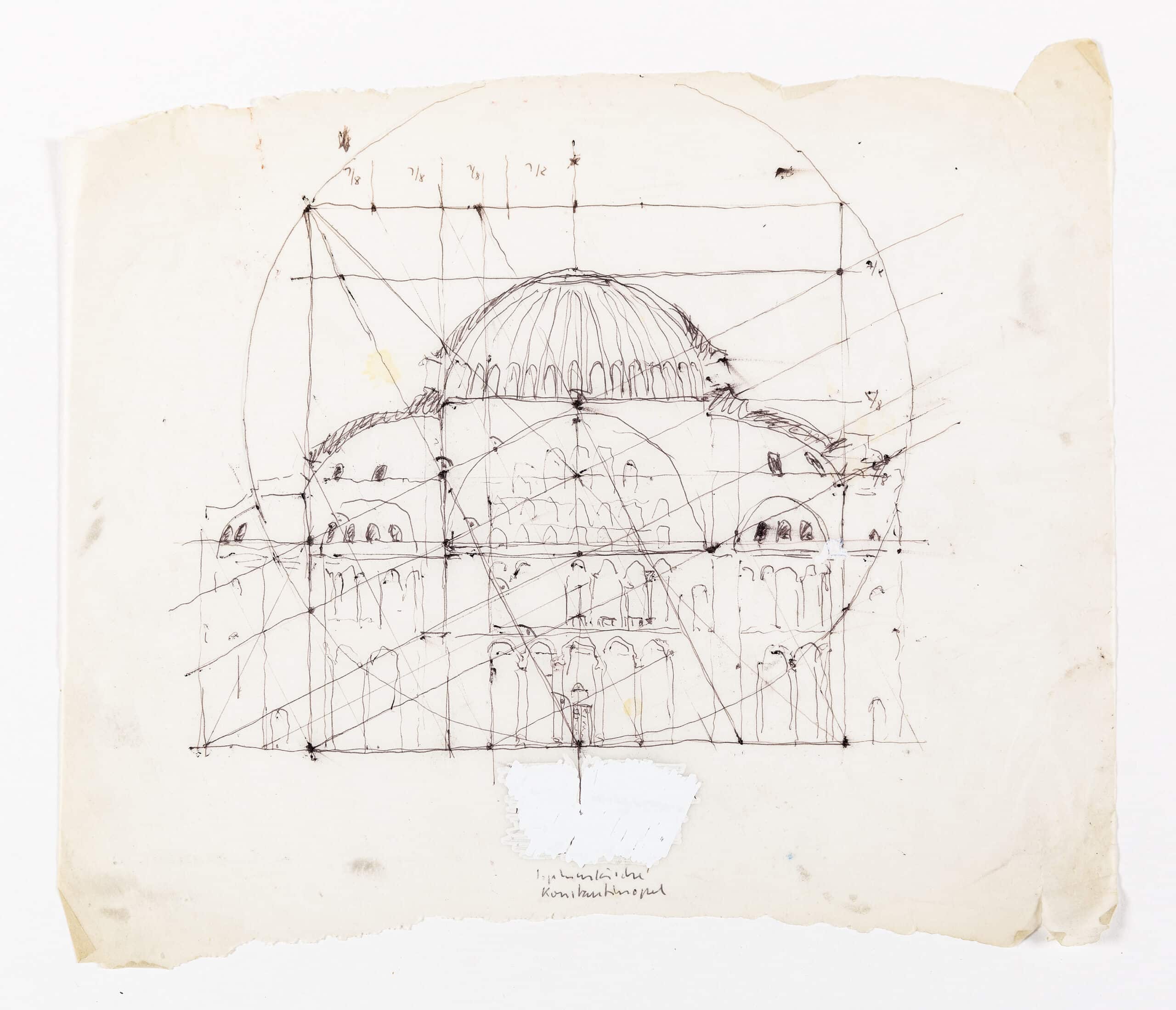
Peter Märkli’s hand-drawn section of the ancient monument Hagia Sophia (532–7) is part of a working process developed alongside his design work. The output is a collection of investigative drawings that document sacred archetypal buildings, and articulate his resolved thesis that ‘architecture has a language’.  

The drawing illustrates a system of proportion inherited from our earliest ancestors. For centuries, proportions were the foundation of the architectural discipline, used on an equal level for sacred, profane and domestic buildings. However, an increasing deviation from the practice of proportions has resulted in contemporary discourse breaking from the past, toward subjective theories of aesthetics. Märkli is aware of this shift, where, as he sees it, the universal language of architecture is dissolving along with human ingenuity, in a society devoted to the service of a purely technical world.

Märkli explains the language of architecture through two overlapping principles: proportion and grammar. Proportion is a system of measurement used to create harmony and rhythm between a building and its constituent parts. It is defined by the equality of ratios between two pairs of quantities. That is to say, proportion determines space in three dimensions through two extremes, and a middle term, usually the mean. Grammar is the appropriate use and refinement of architectural elements, notably the wall, platform, post, and roof. Proportion is therefore inherent to the building, and does not result from personal fancy, but from objective rules. Grammar is the refinement of a building to formalise the structure of a site – its genius loci – and expresses new meanings that are geographic and cosmic (such as history and memory, the climate, changing of seasons, the rise and setting of the sun, and the difference between night and day). Furthermore, Märkli practices and teaches architecture as a discipline. He believes an architect must train to see the language of architecture before beginning to design; just as a musician trains to hear the sounds of music before beginning to compose. [1]

The earliest expressions of a strict mathematical order are recorded in Egypt and Babylon (2500–3000 BCE) in the form of pyramids, ziggurats and tomb chambers. Knowledge of Egyptian and Babylonian thinking is derived from sources drawn on papyrus and inscribed on clay tablets. These treatises depict mathematical inquiries and reveal a process of design that was made visible in architectural form. A surviving branch of knowledge that transcends linguistic and temporal boundaries to universal questions of truth and reason.

Wisdom from Egypt and Babylon was disseminated through maritime trade relations and influenced early art and architecture that emerged in Ancient Greece. The development of the Greek polis (city-state) in the eighth century BCE gave rise to independent political entities. The polis, particularly in Athens, became a setting for experiments in democracy, philosophy and science. A new class of free citizens began to rationally interpret the nature of the universe using mathematical logic. By 550 BCE, through the teachings of the Greek philosopher Pythagoras, geometry had become a theoretical science. 

Pythagoras and his followers believed the entire universe was ordered and governed by numbers, and their observations led to the discovery that music and mathematics share the same fundamental basis. It was this direct relation, between audible harmony in music, and visible order in mathematics, that constituted the chosen ratios and proportions found to be harmonious. In the first instance, this was based on first-hand experience of the sounds associated with numeric variations of pitch. This process crafted a twelve-tone musical scale consisting of five ratios; 12:6 (2:1), 9:6 (3:2), 8:6 (4:3), 144:36 (4:1) and 108:36 (3:1), and three corresponding proportions; arithmetic, geometric and harmonic. The first of these proportions is the arithmetic proportion. Here, the second term exceeds the first by the same amount as the third exceeds the second, such as 2:3:4 or 2:4:6.  The second proportion is called geometric. Here the first term is to the second as the second is to the third, for example, 1:2:4 or 1:3:9. The final proportion is called harmonic. This can be described when the distance of the two extremes from the mean is the same fraction of its own quantity. For example 3:4:6, the mean 4 exceeds 3 by one-third of 3 and is exceeded by one-third of 6. These musical ratios and proportions directly informed the aspiration of architectural form.  

In the wake of Pythagoras, Athenian philosopher Plato, in approximately 360 BCE wrote Timaeus, in which he attempted to explain how the universe and everything in it came into existence. By applying proportion to the solids, he imagined all matter is built up of five regular bodies; earth was associated with the cube, air with the octahedron, water with icosahedron, fire with tetrahedron, and the body of the universe with a dodecahedron. These geometries linked the imperfect physical world with the perfect world of ideas. They illustrated how solid volumes and net shapes, equilateral triangle, square and pentagon, impose rationality onto a whole.  

Pythagorean-Platonic tradition laid the foundation for Euclid’s thirteen-book mathematical treatise titled Elements, published around 300 BCE, which gathered and systematically proved all that was known about geometry. In Book VI, definition 3, Euclid cut a straight line AB in extreme and mean ratio at C, later to be known as the Golden Section, in which the smaller part is related to the larger as the larger is to the whole, in other words AB:AC = AC:CB.

Greek mathematics informed all European systems of proportion that followed. The introduction of the human figure as a proportional reference by the Roman engineer Vitruvius, in the first century BCE, added a rational dimension to the notion of one and the whole. Introduced in his Latin treatise, De Architectura, the simple picture of square and circle overlapping human proportions strengthened the conviction that basic order and harmony lie deep in human nature. 

The principles of proportion were adopted throughout the Byzantine Empire and Middle Ages, through to the Renaissance and Baroque. It is in this context that we find Märkli’s hand-drawn studies. Proportion lost significance during the eighteenth century when it became a matter of individual sensibility and in this respect, the architect acquired complete freedom; an attitude to which most architects operate today. [2] 

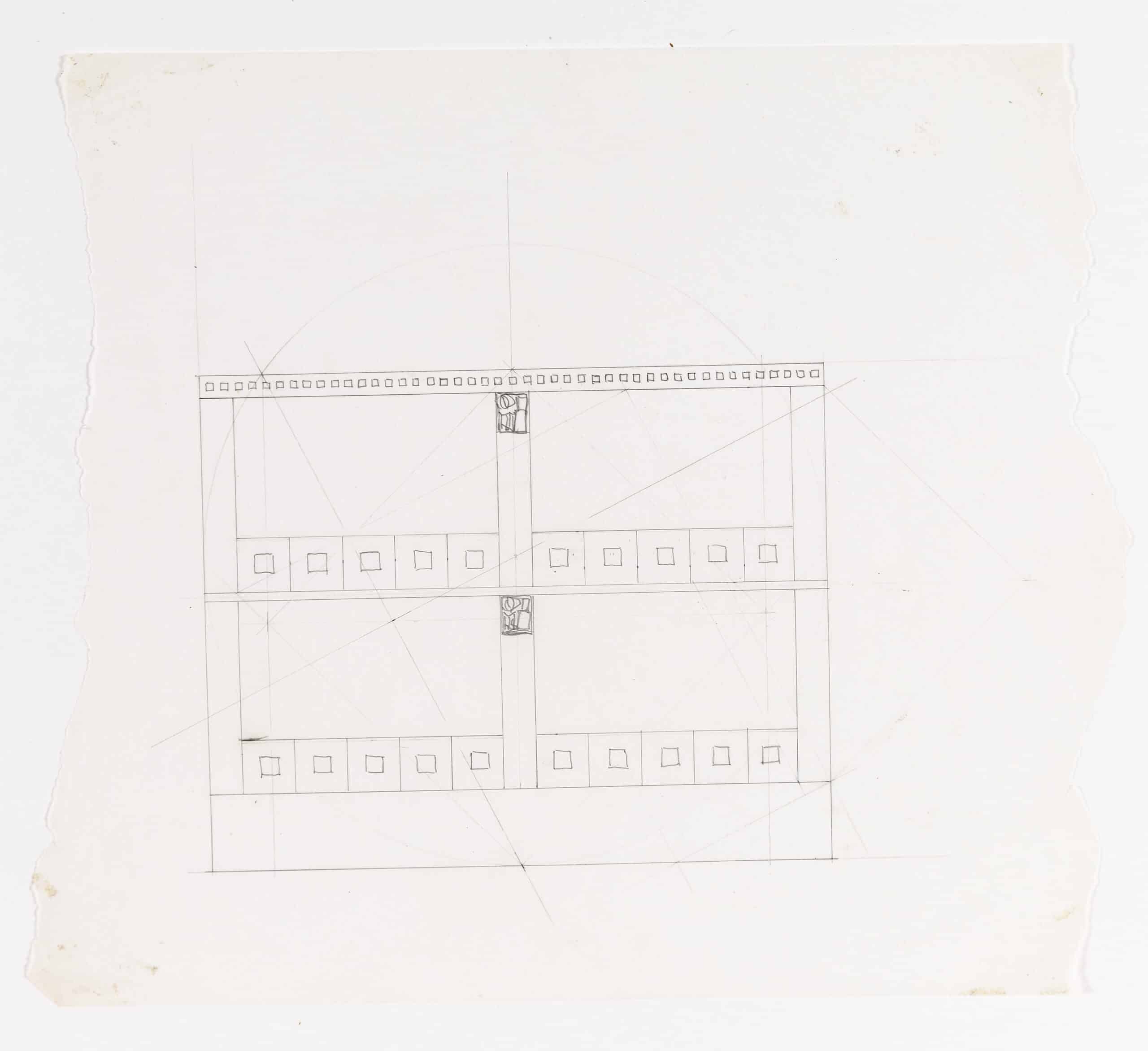
Märkli counters the lost engagement with proportions in twenty-first-century architecture, with an instrument that unites a system of proportion learned through observations of history, with a system of measurement based on geometry and human scale. This is presented in his ballpoint-pen tracing of the Byzantium monument Hagia Sophia.  

The layered image draws lines, shapes and points on top of the historic precedent to communicate certain ratios, and a method of proportion.  Interpreting the lessons set out by Vitruvius, Märkli overlaps square and circle to frame the central volume of the building. The circle intersects the bottom of the square and two upper corners. Its centre is derived from the intersection of two secondary lines that are drawn perpendicular to the midpoints of two primary lines. First, the line for the base of the square, and second, the diagonal line connecting the midpoint of the square’s base to the top left corner. The second perpendicular line intersects the square in a ratio of 7/8 to 1/8 on the right side, and 5/8 to 3/8 on the left side. 5/8 corresponds with the Golden Section down to 7/1000ths, and 7/8 relates to the sine ratio of an equilateral triangle within 9/1000ths. This highlights two key components of proportion attested to throughout history. [3] 

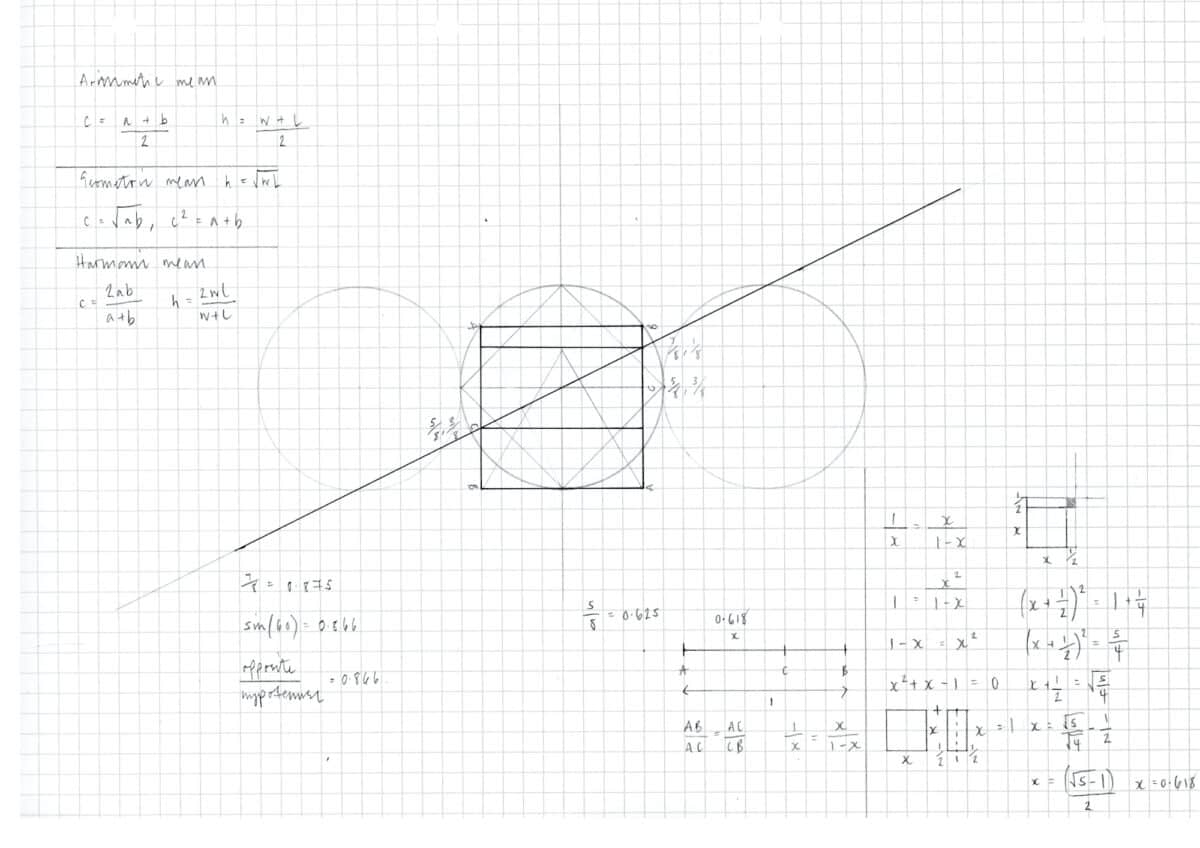
The sectional nature of the drawing, overlaid by the symmetrically scalable 8 unit square, reveals the unit length and height of the central volume. Length is 8, and height is 5 to the base of dome, and 7 to the top of dome.  However, for true proportion there must be a third dimension, in this case the width is missing. This can be calculated using the three types of proportion established by Pythagoras in music and developed during the Renaissance. When the height of the room is understood to be the mean, 5 or 7, the width is 2 or 6 in arithmetic proportion; 3.125 or 6.125 in geometric proportion; 3.63 or 6.2 in harmonic proportion [4].  

Surveyed plans of Hagia Sophia reveal the main space width is roughly 3.65, 2/100ths shy of 3.63. This reveals the volume, to the base of dome, is harmonically proportioned and implies Märkli uses this type of proportion as an ideal when designing [5].

The language of the architecture illustrated is not a return to antiquity, it is the art of historical translation, so to imagine something new for the future using a universally valid method.  Proportion and grammar are tools to communicate – a means of taming the arbitrary and chaotic with order and structure that can be traced back to our oldest ancestors.

Stacey Lewis is currently studying for her part three in architecture in London.

This text was entered into the 2020 Drawing Matter Writing Prize. Click here to read the winning texts and more writing that was particularly enjoyed by the prize judges.

Notes

1.  The introduction is derived from ideas in the following source: Imoberdorf, Chantal. Märkli: Chair of Architecture at the ETH Zurich 2002-2015. Zürich: Gta Verlag, 2016.
2. The historical context section refers to dates and ideas written in the following sources: Fletcher, Banister. A History of Architecture. London: Routledge, 1996, twentieth edition; first published 1896; Wittkower, Rudolf. Architectural Principles in the Age of Humanism. Chichester: Academy Editions, a division of John Wiley & Sons, 1998, fifth edition; first published in 1949.
3.  This paragraph paraphrases Märkli, Peter. Interviewed in: Gerber, Andri., Joanelly, Tibor., & Atalay Franck, Oya. Proportions and Cognition in Architecture and Urban Design: Measure, Relation, Analogy. Berlin: Dietrich Reimer Verlag, 2019, pp.118-119.
4. Mean formulas: arithmetic mean h = w+l ÷ 2, geometric mean h = wl, harmonic mean h = 2wl ÷ w+l, where h is the height, l the length, and w the width of room.  Formulas cited in: Mitrovic, Branko. Palladio’s Theory of Proportions and the Second Book of the Quattro Libri dell’Architettura. Journal of the Society of Architectural Historians, September 1990, p.279.
5. Hagia Sophia dimensions taken from: Fletcher, Banister. A History of Architecture, p.303.